קינמטיקה

קינמטיקה היא התחום בפיזיקה המתאר תנועת גופים במרחב, כלומר חיזוי המשך התנועה על פי תנאי ההתחלה. הקינמטיקה אינה עוסקה בכוחות הגורמים לתנועה זו (תחום הכוחות נקרא – דינמיקה).
ניתן לחלק את הקינמטיקה לתנועה שוות תאוצה, בה ניתן לתאר את תנועת הגוף ע״י מספר מצומצם של משוואות, ולתנועה בתאוצה משתנה, בה החישוב מורכב יותר ודורש עבודה עם אינטגרלים.
תחום נוסף של קינמטיקה נקרא בליסטיקה, בו בעזרת משוואת מסלול נתאר את המסלול אותו הגוף עובר, ללא תלות בזמן.

נוסחאות קינמטיקה

 
למשוואות הקינמטיקה מגיעים בעזרת אינטגרל על מיקום. כלומר, אם גוף נע בתאוצה קבועה, בעזרת אינטגרל נקבל את מהירותו ובעזרת אינטגרל נוסף נקבל את מיקומו. לקבלת נוסחת המהירות נרשום:

v_{(t)}=\int a\cdot dt=v_0+at

כלומר, אינטגרל על התאוצה ייתן את משוואת המהירות (כאשר המהירות ההתחלתית היא קבוע האינטגרציה של .
האינטגרל).
כעת, נבצע אינטגרל על המהירות לקבלת נוסחת המיקום:

x_{(t)}=\int v_0+at=x_0+v_0t+\frac 12at^2

(כאשר המיקום ההתחלתי הוא קבוע האינטגרציה של האינטגרל).

משוואת המיקום תחת תאוצת גרביטציה:
תנועת גוף חופשי מוגדרת כגוף הנע תחת כוח הגרביטציה בלבד. משמע, לגוף יש תאוצת גרביטציה בציר האנכי, ואין לו גרביטציה בציר האופקי. משוואות המיקום לכל ציר יהיו כעת:

\textcolor{blue}{x_{(t)}=x_0+v_{0\hat x}t } \\
\textcolor{orange}{y_{(t)}=y_0+v_{0\hat y}t -\frac 12gt^2}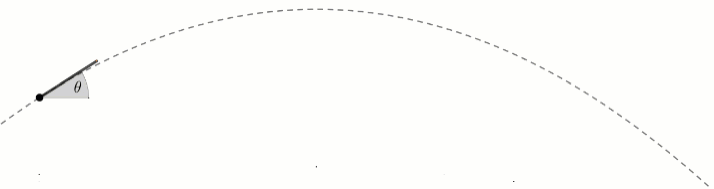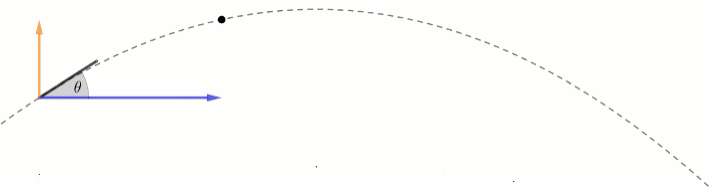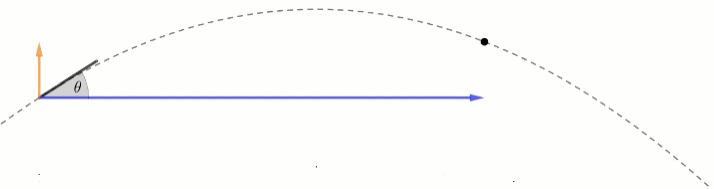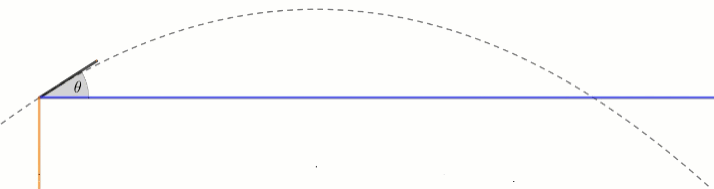

בעזרת שתי משוואות אלו נוכל לתאר את מיקומו של הגוף בזמן כפונקציה של נתוני ההתחלה.
את המהירות ההתחלתית בשני הצירים נוכל גם לכתוב בעזרת גודל וכיוון כך:

v_{0\hat x} = v\cdot cos(\theta )\\v_{0\hat y} =v\cdot sin(\theta)

כשהזווית מוגדרת כזווית בין כיוון המהירות לבין הציר האופקי.

משוואת המסלול:
ממשוואות המיקום בזמן נוכל לחלץ את משוואת המסלול: (אם יש לנו מיקום בציר אנכי כפונקציה של זמן ויש לנו מיקום בציר אופקי כפונקציה של זמן נוכל לקבל מיקום בציר אנכי כפונקציה של מיקום בציר אופקי)

y_{(x)}=x\cdot tan(\theta)-\frac12g[\frac{x}{v_0\cdot cos(\theta)}]^2

משוואה זו תתאר לנו את מסלולו של הגוף, ללא תלות בזמן.