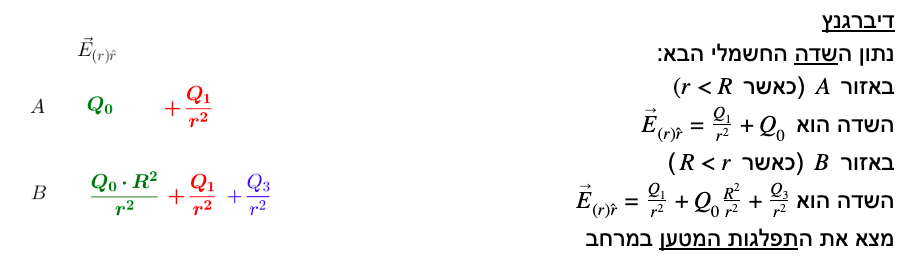דיברגנץ
פעולת הדיברגנץ מחשבת בעזרת התפלגות השדה החשמלי במרחב את צפיפות המטען במרחב (שיצרה את אותו שדה). להבנה אינטואיטיבית של הפעולה נזכר בדרך הפעולה ההפוכה:
למדנו את נוסחת המעבר מהתפלגות מטען להתפלגות שדה (בקואורדינטות כדוריות בדוגמא הבאה):
E_{(r)}=\frac 1{r^2}\int\rho_{(r)}\cdot r^2drלכן, לחישוב התפלגות המטען לפי השדה, נבודד את הנעלם כך:
נכפול את שני האגפים במרחק בריבוע ונקבל
r^2\cdot E_{(r)}=\int\rho_{(r)}\cdot r^2drנגזור (לפי מיקום) את שני האגפים ונקבל
\frac{r^2\cdot E_{(r)}}{dr}=\rho_{(r)}\cdot r^2ונחלק במרחק בריבוע לקבלת נוסחת הדיברגנץ:
\frac{1}{r^2}\frac{r^2\cdot E_{(r)}}{dr}=\rho_{(r)}בנוסף נכיר, כי את פעולת הדיברגנץ נהוג לרשום בעזרת האופרטור נבלה (משולש הפוך) עם נקודה אחריו
\frac{1}{r^2}\frac{r^2\cdot E_{(r)}}{dr}=\nabla \cdot E