כבידה – סיכום
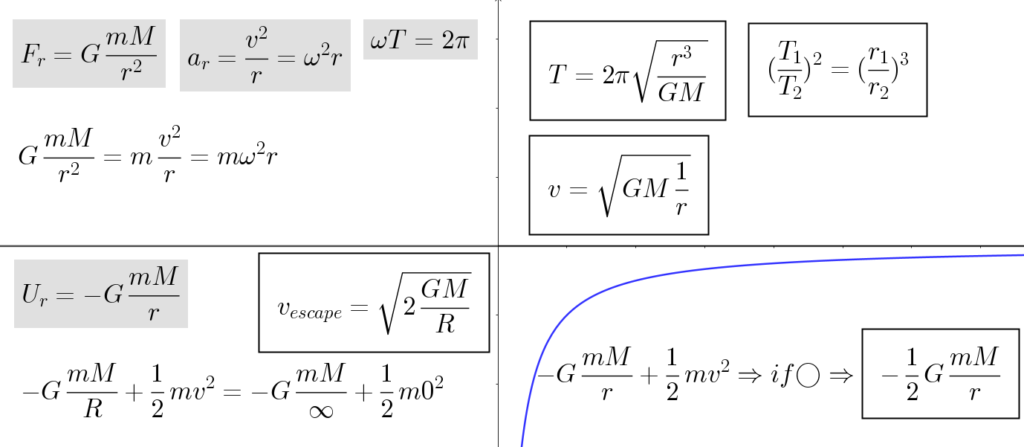
כאשר מתרחקים מכדור הארץ, נוסחת כוח הכובד ״מוחלפת״ בנוסחה חדשה בה יש תלות בין הכוח למרחק מכדור הארץ. פיתוח כוח זה ייתן לנו תיאור של תנועת לוונים בחלל.
כוח זה אם כן יהיה הפוך לריבוע המרחק בין הגופים, לפי הנוסחה:
F_{\hat r}=G\frac{m_1m_2}{r^2}
לחישוב האנרגיה הפוטנציאלית של כוח זה נבצע אינטגרל על הכוח ונקבל את האנרגיה:
U_g=-G\frac{m_1m_2}{r}
כעת, נוכל להשתמש בנוסחאות אלו כדי לתאר תנועה של לווין. נתאר תחילה מקרה פשוט, בו תנועת הלווין היא מעגלית, ואחר כך נעבור לתנועת לווין כללית (לאו דווקא מעגלית).
תנועה מעגלית של לווין
תנועה זו היא התנועה הפשוטה ביותר לתיאור. מהצבת כוח הגרביטציה לנוסחת התאוצה הרדיאלית במעגל נקבל קשר בין רדיוס המעגל לבין מהירותו.
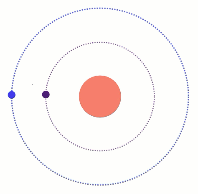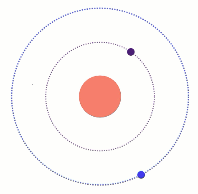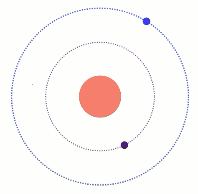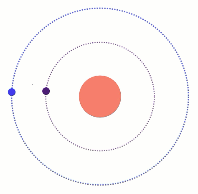
v^2=\frac{GM}{R}
ומהצבת קשר זה בנוסחת האנרגיה נקבל כי האנרגיה של הלויין תהיה:
E_k=-\frac12G\frac{mM}{R}=-\frac12U_g
תנועה כללית של לווין
לווין, מעצם הגדרתו, נע תחת כוח מרכזי (כוח הגרביטציה) וככזה, תנועתו תהיה אליפטית (מסוגים שונים עליהם נלמד בהמשך). בתנועה זו לא יהיה שימוש בנוסחאות הרלוונטיות לתנועה מעגלית, ובמקומן נשתמש בחוק שימור התנע. חוק זה יכתיב את הקשר הבא:
v_1r_1\cdot sin(\theta _1)=v_2r_2\cdot sin(\theta _2)
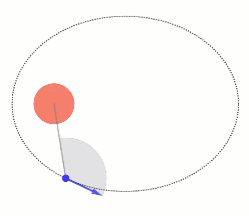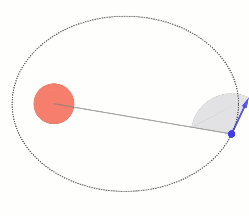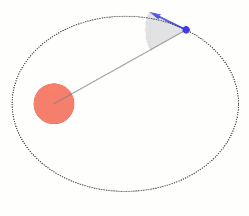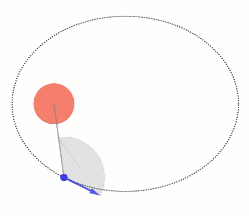
בה נשתמש כשנרצה לתאר את כיוון התנועה (או זווית התנועה).
במקרים רבים אחד הנתונים ידבר על הנקודה הקרובה ביותר או הרחוקה ביותר באליפסה (נקראות: אפוג׳י ו-פריג׳י) שם זווית התנועה מאונכת.
הצבת קשר זה בנוסחת האנרגיה תניב את הנוסחה הבאה:
v_1^2-v_2^2=2GM(\frac1{r_1}-\frac 1{r_2})סוגי תנועות
האנרגיה שיש למסה תכתיב את צורת התנועה. באנרגיה מסויימת התנועה תהיה מעגלית. אם נקטין או נגדיל את האנרגיה צורת התנועה תהיה אליפטית.
חשוב לשים לב לשלושה מסלולים:
1 – אליפסה רגילה
2 – אליפסה החותכת את כדור-הארץ
3 – אליפסה שהולכת לאינסוף
במקרה בו נרצה לירות גוף מכדור-הארץ ולהכניסו למסלול שיתנתק מכדור הארץ (אליפסה שהולכת לאינסוף) ניתן לו מהירות הנקראת מהירות מילוט, ובהצבה בנוסחאות הקודמות נקבל:
v^2_{escape}>2\frac{GM}{R}